The magnetic field produced by an infinite wire with current
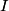 is is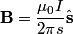 where 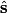 is a unit vector in the azimuthal direction determine by the right-hand rule. So, the magnetic field at is a unit vector in the azimuthal direction determine by the right-hand rule. So, the magnetic field at 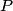 due to the wire in the due to the wire in the 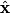 direction will be out of the page, and the magnetic field at direction will be out of the page, and the magnetic field at 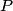 due to the wire in the due to the wire in the 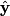 direction will be into of the page, and both will have the same magnitude, so they will cancel. Therefore, answer (E) is correct. direction will be into of the page, and both will have the same magnitude, so they will cancel. Therefore, answer (E) is correct. |